一 教学重点:集合的基本概念
元素与集合的关系
二 教学难点:元素的特性
三 教学目标 :能辨析对象是否能构成集合
能正确判断给定元素与集合的关系
知记数学中常用数集及其记法
四 教学过程:
(一)引入:在衔接课程中,我们已经初步接触了数的集合,比如  的解集,全体的自然数;这些都是数的集合;在初中我们还学过圆,Q1:什么是圆?(到定点的轨迹等于定长的点的轨迹),这样的所有点组合在一起我们称之为圆。
的解集,全体的自然数;这些都是数的集合;在初中我们还学过圆,Q1:什么是圆?(到定点的轨迹等于定长的点的轨迹),这样的所有点组合在一起我们称之为圆。
Q2:那我们生活中有没有集合的例子?
(班级,军队等等)
夸。(新颖/贴近生活/这个我没想到/有趣)好接下来我们一起看一些其他例子,归纳出集合的共性。
(二)新知:书,第二页8个例子
这8个例子的研究对象有数,卫星,汽车国家等,我们把研究对象称之为元素。
请学生进行分类,元素为数的有:(1),(7)。元素为点的有:(6)。讲解(6)中点构成的图形是两条平行线。
(2)的元素是:金星汽车厂2003年生产的每一辆汽车
把一些元素组成的总体称做集合,(5)中的集合是所有正方形。观察这些例子,发现集合中的元素可以是点,可以是数,也可以是人和物。
Q3:那我们班身高较高的同学可否组成一个集合?(能/不能)
随机请两位同学,说一说他们认为高于一米几是高。
也就是说身高较高的同学没有明确的标准,而前8个例子都给出了确定的范围,于是我们得到了集合的第一个特性:确定性。
例1:考察下列每组对象,能构成一个集合的是——
①某校高一年级成绩优秀的学生
②直角坐标系中横纵坐标相等的点
③不小于3的自然数
④2016年第31届奥运会金牌获得者
练习1:给出下列说法:
①中国的所有直辖市可以构成一个集合
②高一(1)班较胖的同学可以构成一个集合
③正偶数的全体可以构成一个集合
④大于2011且小于2016的所有整数不能构成集合
其中正确的有——
第二,我们要求一个给定的集合,其中的元素是互不相同的,也就说集合中的元素是不重复出现的,我们称它为互异性。
比如{1,1,2}是一个集合吗?(不是)
那再来看
如果上述表达构成一个集合,求a的取值范围。
互异性在参数问题中起到至关重要的作用。
最后,再来看一个集合:高一9班的全体学生。Q4:当我把靠窗的一组和靠门的一组对调后,这个集合发生变化了吗?(没有)
因为班级里的人没变,构成集合的元素没变,可顺序变了啊?(不影响)
集合中元素的顺序不影响集合,也即集合具有无序性。
{1,2,3}和{3,2,1}这个集合相同吗?(相同)
因为集合中元素相同,于是我们一起来总结下,集合相同,我们只需——集合中元素相同。以后学习中,集合用大写字母A,B,C表示,元素用a,b,c表示。
如果给定了一个集合,比如A={1,2,3},给定了一个元素,元素与集合的关系只有两种,1在集合中,我们说1属于集合A,用  表示,2不在集合中,我们说2不属于集合A,用
表示,2不在集合中,我们说2不属于集合A,用  表示。
表示。
注意:属于符号具有方向性,开口永远朝着集合,写的时候左边永远是元素,右边永远是集合。
练习2:书第三页练习题第一题。
数学中常用数集都具有各自的记法:
自然数集——N——natural number
正整数集——N*、N+
实数集——R—— real number
有理数集——Q——所有能写成分数的数,即两个数的商——queotient
整数集——Z——唯一一个与德语相关——为了纪念德国女数学家对环理论的贡献,用德文中整数单词zahlen的首字母表示整数集
(三)教学活动
班级分为四组,每组推举8名同学,做接龙游戏。
比如老师拿出7,第一位同学反应0属于集合N;第二位同学重复并接龙0属于N且0属于Z;第三位同学0属于N且属于Z且属于Q,第四位同学0属于N 且属于Z且属于Q且属于R。第五位同学要喊出下一个,并从这位同学开始下一个数。
要求:(1)元素与集合之间一定要说属于。
(2)说包括元素的集合时,一定要从最小范围开始说起
(3)遇到在你处接龙结束时,一定快速反应下一个,老师才会给出下一个大佬们都在玩{精选官网网址: www.vip333.Co }值得信任的品牌平台!
(4)每组一次犯错机会
(四)小结
元素的定义,集合的特性,元素与集合的关系,常见数集的记法。
(五)教后记
①接龙游戏很成功。
②形容元素时要注意:“每一个";形容集合时要强调:"所有"以及所给的范围或时间;互异性所举的参数例子,全部来自何老师的课堂大佬们都在玩{精选官网网址: www.vip333.Co }值得信任的品牌平台!。
③将常用数集的记法与英文含义结合来自我师父王老师的建议。
专栏的第一篇教案,感谢以上两位老师毫无保留的指点,我一直记得初衷,与各位共勉。
文章声明:以上内容(如有图片或视频在内)除非注明,否则均为乐球直播_乐球直播免费体育直播_乐球直播nba免费观看高清_24直播网原创文章,转载或复制请以超链接形式并注明出处。
本文作者:admin本文链接:https://yacai158.com/post/104.html


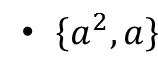


还没有评论,来说两句吧...